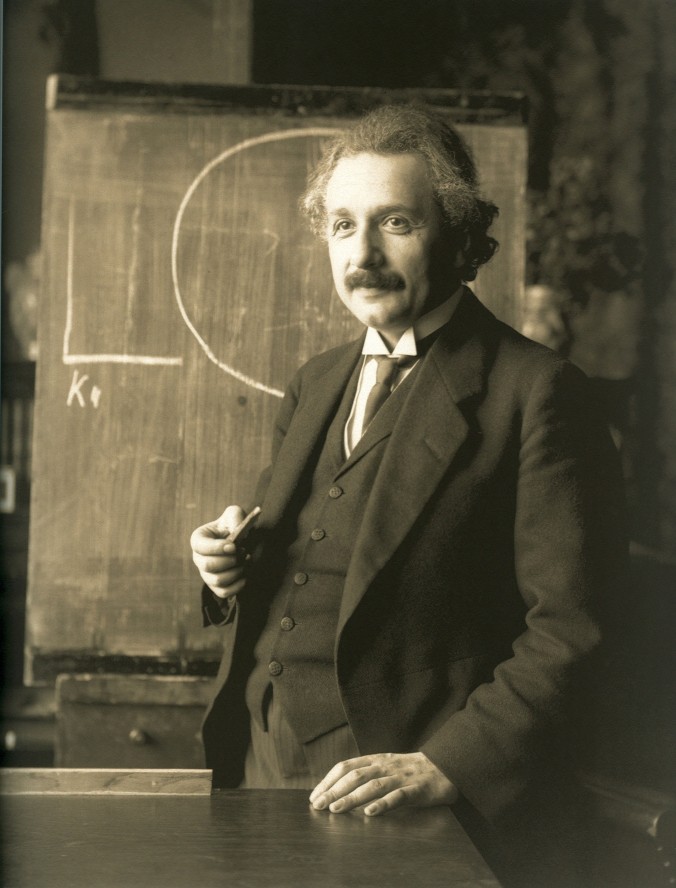This year, professional physicists and the few geeks who are still interested in science (should we call them nerds?) are celebrating General Relativity’s centenary.
Great. What of it then?
General Relativity breaks the record for flowery adjectives in science. It has been described as impossible to understand, poetic, beautiful, elegant and simple.
Surely it’s elegantly simple?

Simple? Einstein’s Zurich notebook. He makes a wrong assumption about weak gravitational fields on this page, and ends up the wrong path. He starts again on the next page, and arrives at the correct solution.
It’s hard to define ‘simple’ in scientific language. I more appropriate (and sober) description would be ‘complete’. General Relativity is the most complete theory of gravity known so far.
Why is it complete?
Because all gravitational phenomena we have observed so far can be modelled by General Relativity. It describes everything from falling apples, to the orbit of planets, the bending of light, the dynamics of galaxy clusters, and even black holes. The domain of validity of the theory covers a wide range of energy levels and scales. And scale is what physics is all about.
When the BICEP-2 experiment claimed to observe gravitational waves, there was a deeper (and probably more significant) result. It meant that General Relativity is valid up to the GeV energy scale, almost reaching the domain where quantum physics becomes the preferred description.
Can it describe the whole Universe?
Almost. Modern cosmology is based on General Relativity applied to a simple model of the Universe.
We have the field equations for gravity: the Einstein field equations.
We have the boundary conditions: homogeneity and isotropy, and the contents of the four-dimensional spacetime – matter or energy.
Put them together and you obtain a metric. Think of it as a generalised gravitational potential for the entire Universe.
Almost? What’s the catch?
The big questions in physics (we should really say Big Questions – they’re that important) , on this 100th birthday of General Relativity are the things that cannot be explained by this model: Dark Energy (the Universe doesn’t just expand, it accelerates), and Inflation (the initial the matter-energy distribution was not homogeneous).
Einstein published most of his papers on General Relativity in 1914. Why are we celebrating 2015?
Because the essential element of General Relativity is the field equations. Einstein had been working on the problem for some years, starting in 1907. He arrived at the final, correct form in 1915. And he was fully aware of the significance of this publication. He called it simply ‘The Field Equations of Gravitation’ (‘Feldgleichungen der Gravitation’, in Akademie der Wissenschaften, Sitzungsberichte 1915 (part 2) pages 844-847).
From then on, it was a matter of working out the derivations.

Manuscript of ‘Grundlage der allgemeinen Relativitätstheorie’ (The Foundation of the General Theory of Relativity).