Machine learning is full of picturesque terminology which has accumulated over the years to create a mystique around the subject (and the industry). This despite the fact that many of the concepts already had perfectly suitable names that had been around for years (sometimes centuries). Let us start our journey with one such term: perceptrons.
Just what are perceptrons?
Category: Uncategorized (Page 1 of 4)
Einstein presented the equations which define the theory of General Relativity in November 1915. The Einstein field equations, as they are known, specify how the geometry of space and time behaves in the presence of matter and energy.
If we know the content of the universe, and if we consider the universe at scales where gravity is dominant, these equations can be used to obtain a description of spacetime over the whole universe. This is one of the most useful features of General Relativity.
Modern cosmology began in Russia in the 1920s with the work of Alexander Friedmann. Using General Relativity, Friedmann showed that a universe which was homogeneous and isotropic should either expand or contract.
At the time, Friedmann’s work was not widely recognised, and he was initially criticised by Einstein himself, who thought he was in error. Einstein developed an alternative model of the universe, which he forced to be static by introducing a term in his equations called the cosmological constant.
We now know that the universe is expanding. How could a great scientist like Einstein make such an error?
We need to go back to the early 20th century. At the time, most observations of the universe were limited to stars in our own Milky Way galaxy, which have low velocities. So the universe appeared to be static.
The scale of the universe was another open question. Astronomers were not even sure that the universe contained other galaxies beside our own. Catalogues of astronomical objects contained objects known as spiral nebulae, but their nature was not yet entirely understood. Were they other galaxies outside our own, or were they gas clouds inside the Milky Way? Did the cosmos consist entirely of the Milky Way? This debate raged throughout the 1920s.
The first challenge to the static universe theory came in 1917, when Vesto Slipher measured the spectra of spiral nebulae. He showed that the light they emitted was shifted towards the red. This meant that they were receding from us.
In 1919, the Hooker Telescope was completed. Located at the Mount Wilson Observatory in California, it had a 100-inch aperture, larger than any telescope at the time. Soon after, an astronomer by the name of Edwin Hubble started working at the observatory. He was to make two revolutionary discoveries which changed the scientific view of the universe.
Using the powerful new telescope, Hubble was able observe the spiral nebulae and measure their distances with unprecedented accuracy. In 1924, he showed that they were too distant to be part of the Milky Way, and thus proved conclusively that the universe extended far beyond our own galaxy.
In 1929, Hubble made another remarkable discovery. He obtained the spectra of many galaxies and calculated the relative velocities of the galaxies from the Doppler shifts of spectral lines. All of the galaxies except for a few of the closest displayed redshifts, and thus are receding from us.
What was more, the relationship between the distance and the velocity was a simple linear one. The picture below shows Hubble’s original graph. The points all lie close to a straight line. In other words, the velocity of a galaxy (v) is proportional to its distance (d):
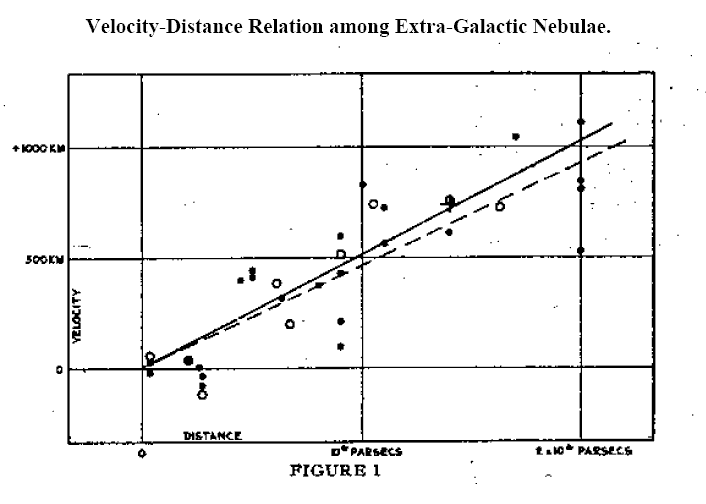
This equation later became known as Hubble’s Law. The constant of proportionality H is known as the Hubble constant.
But these observations did not explain the reason for the recession of the galaxies. Why should galaxies move away from each other? The answer was to come from Einstein’s theory itself.
When we solve Einstein’s field equations, we obtain a mathematical quantity called a metric. The metric may be thought of as a description of spacetime under certain conditions, in the presence of matter and energy.
In 1927, two years before Hubble’s discovery, a Belgian priest and physicist named Georges Lemaître predicted the redshift-distance relation using Einstein’s equations for General Relativity applied to a homogeneous and isotropic universe. The problem was explored further in the 1930s by the mathematicians Howard P. Robertson in the US and Arthur Geoffrey Walker in the UK.
The combined work of these scientists proved that the only metric which can exist in a homogeneous and isotropic universe containing matter and energy – in other words, a universe very much like our own – is the metric for an expanding or contracting universe.
You will notice how the results leading to the exact solutions of Einstein’s equations for such a universe required the combined effort of many scientists. In fact, such solutions are known as the Friedmann-Lemaître-Robertson-Walker metric, or FLRW metric.
We now had an explanation for the observed redshifts of the galaxies. It is caused by the expansion of the universe itself, and the expansion rate is given by the Hubble parameter. The value of this parameter gives us vital information about the evolution of the universe. It is one of the most important quantities in modern cosmology.
In the face of such overwhelming evidence for a dynamical, expanding universe, Einstein dropped his support for the cosmological constant, calling it “the biggest blunder” of his life.
The story does not end here. Astronomers kept observing the universe, measuring the distances and velocities of various objects such as galaxies, galaxy clusters and supernovae, and developing new and improved instruments and methods to measure the Hubble constant. More than seventy years after Edwin Hubble, we made new discoveries which show that Einstein did not make a blunder, and he may have been right about the cosmological constant after all, but for a different reason.
The documentation on the IN2P3 Computing Centre portal does not contain any information specific to MontePython. Boris Bolliet provides some very useful instructions on his website. Aside from this, there is nothing at all. So I thought I would provide a few tips, especially for Euclid consortium members.
If you are a member, you can request an account on the cluster.
The first thing to do is to create a folder on /sps/euclid/Users/. You may choose any name (e.g. your username: /sps/euclid/Users/username).
In order to use MontePython, you will need to install software packages. Just follow the instructions on Boris Bolliet’s page.
The tricky bit is the job submission script. I am grateful for Quentin Le Boulc’h for what follows. We spent a lot of time trying to pin down the right parameters for the resource options.
You have two options.
Option 1
#!/bin/sh
#$ -N yourscript
#$ -P P_euclid
#$ -q pa_long
#$ -l sps=1
#$ -j n
#$ -l os=cl7 -pe openmpi 4
#$ -o $JOB_ID.out
#$ -e $JOB_ID.err
export OMP_NUM_THREADS=1
source /pbs/home/y/yourusename.profile
source /usr/local/shared/bin/openmpi_env.sh
mpirun -np $NSLOTS montepython/montepython/MontePython.py run etc.
Option 2:
#!/bin/sh
#$ -N yourscript
#$ -P P_euclid
#$ -q pa_long
#$ -l sps=1
#$ -j n
#$ -l os=cl7 -pe openmpi_8 32
#$ -o $JOB_ID.out
#$ -e $JOB_ID.err
export OMP_NUM_THREADS=8
source /pbs/home/y/yourusename.profile
source /usr/local/shared/bin/openmpi_env.sh
mpirun -np 4 -pernode montepython/montepython/MontePython.py run etc.
Why would you need to avoid entering a password when you use SSH? Typing in your password each time you log in is tedious. You may also need to call ssh from within a shell script.
These instructions are not specific to the APC computing cluster (APCSSH and APCCLM) . They will work on any Unix-like operating system.
You already have an APC account with a login name, which I shall call APClogin. I assume you have already succesfully logged into your APC account using your password. Write down your password somewhere, case you need it.
If you are using Mac OS X, you can do all of the steps below in Terminal. If you are using Windows, you need an ssh client such as PuTTY .
LocalLogin stands for the login name on your local machine.
Here’s how to do it.
1: Generate the authentication keys
Type the following in your terminal window.
$ ssh-keygen -t rsa
You will get a message saying:
Generating public/private rsa key pair.
Enter file in which to save the key (/Users/LocalLogin/.ssh/id_rsa):
If you wish to change the default location, go ahead and specify a file path. Better to keep it simple, and just press Enter.
You will get this message asking for a password (“passphrase”). Do not enter one. Just press Enter, twice.
Enter passphrase (empty for no passphrase):
Enter same passphrase again:
If you did everything properly you will get a message giving the file path to the keys, and the key fingerprint:
Your identification has been saved in /Users/LocalLogin/.ssh/id_rsa.
Your public key has been saved in /Users/LocalLogin/.ssh/id_rsa.pub.
The key fingerprint is:
SHA256:dWitjNhmrttyt7oCFmYdsu6wdA6Y5yao8UuoZ7Zzgnjsi22Q LocalLogin@apcdhcp24.in2p3.fr
The key's randomart image is:
+---[RSA 2048]----+
| |
| . |
| . . O .|
| . o o O + |
| S o B * =|
| ... . + o = = |
| Ho. . o = . .|
|o=+O.o .. o + o |
|o=O+*. ..+ .|
+----[SHA256]-----+
2: Create a .ssh directory on apcssh
Next, you need to create a .ssh directory on apcssh.in2p3.fr by typing:
$ ssh APClogin@apcssh.in2p3.fr mkdir -p .ssh
You will be asked for your password (that is why you need to have it written down somewhere). Type it in.
APClogin@apcssh.in2p3.fr's password:
3. Append your local public key to the authorised keys on apcssh
Enter the line below. You will then be asked for your password, which you need to enter.
$ cat .ssh/id_rsa.pub | ssh APClogin@apcssh.in2p3.fr 'cat >> .ssh/authorized_keys'
APClogin@apcssh.in2p3.fr's password:
4. Done
Now you should be able to log into apccsh.in2p3.fr using the usual ssh command without entering a password.
Doing the same for the APC cluster
If the above works, you can log into apcclm following the same steps, except that you need to log into apccssh first.
In summary:
1. Log into apccsh (which you can now do without a password)
2. Generate the authentication keys
3. Create a .ssh directory on apcclm by typing
$ ssh APClogin@apcclm mkdir -p .ssh
4. And you’re done
The official documentation is here http://monte-python.readthedocs.io/en/latest but it glosses over some important details. You may find more information here: http://www.iac.es/congreso/cosmo2017/media/montepython.pdf
Installing Montepython
Installing Montepython is quite straightforward if you follow the installation guide. Just make sure that that your version of Python is 2.7. There are some syntax changes in Python 3 which prevent the code from installing.
Running Montepython
Running Montepython on your local machine is easy if you follow the official documentation. For the code to be any use, however, you need to output chains with thousands of points. And that means running it on the APC cluster.
Here are some helpful tips.
The graphical backend
Montepython and the CLASS Python wrapper use Matplotlib. You need to log in with the -Y option for both apcssh and apcclm:
$ ssh -Y APClogin@apcssh.in2p3.fr
followed by
$ ssh -Y apcclm
When you run Montepython on the cluster using a script, you will need to set this environment variable in the script itself (see below).
External programs within CLASS
If you modify CLASS by calling an external program (let’s call it PowerSpectrumExtension.py) to calculate some quantity, remember to make it executable by running
chmod +x PowerSpectrumExtension.py
Job submission
You need to write a script that gets the job done. This is described here https://www.apc.univ-paris7.fr/FACeWiki/pmwiki.php?n=Apc-cluster.Scheduler.
When you run jobs on a cluster, you are sharing resources with the other users. If you ask for resources (memory, number of nodes) that are unavailable, or ask for too much, your job will be sent to the back of the queue, or aborted.
Here’s an example of a message for an aborted run:
There are not enough slots available in the system to satisfy the 4 slots
that were requested by the application:
Montepython.py
Either request fewer slots for your application, or make more slots available
for use.
You also need to set the right environment variables for the required libraries
This is an example of a script which ran succesfully on the APC cluster:
#!/bin/bash
#PBS -N JOBNAME
#PBS -o $PBS_JOBID.out
#PBS -e $PBS_JOBID.err
#PBS -q furious
#PBS -m bea
#PBS -M name.surname@apc.univ-paris7.fr
#PBS -l nodes=1:ppn=32,mem=64GB,walltime=200:00:00
export SCRATCH="/scratch/$USER.$PBS_JOBID"
export PATH=/usr/local/openmpi/bin:$PATH
export OMP_NUM_THREADS=8
export LD_LIBRARY_PATH=/usr/local/openmpi/lib/:/usr/local/openmpi/lib/openmpi/:$LD_LIBRARY_PATH
set -e
cd ~/montepython
/usr/local/openmpi/bin/mpirun -np 4 env MPLBACKEND=Agg montepython/Montepython.py run -p input/lcdm.param -o chains/planck/lcdm -N 20000 --silent
The –silent command suppresses Montepython’s screen output (which you don’t need when you submit a cluster job).
Here are some good resources explaingin qsub settings:
https://hpcc.usc.edu/support/documentation/running-a-job-on-the-hpcc-cluster-using-pbs
http://www.arc.ox.ac.uk/content/pbs
Analysing the chains
Once the run has terminated, output the plots and information by running:
cd montepython
env MPLBACKEND=Agg montepython/Montepython.py info [path]/[to]/[chains]/*.txt --want-covmat
The option –want-covmat outputs the covariance matrix.
Make sure to include env MPLBACKEND=AGG or you will get the usual matplotlib display problems.
Data visualisation is, we are told, the hottest keyword in data science. Like many items of jargon fashionable in these modern times (just like the phrase ‘data science’ itself), its meaning is at best vague. The tech industry like to think of data visualisation as somehow computer-related, or the final stage of a process of computation and data manipulation which involves coding or the use of software tools. But human beings have been manipulating data and doing data science for millennia, so it follows that the history of data visualisation goes back a long way, long before computers were invented.
Consider graphs, the most common form of data visualisation. A graph is a visual representation of the relation between two variables (I mean the kind that’s plotted on a flat surface).
Who drew the first graph?
In 1936, Howard Gray Funkhouser described an image in a manuscript discovered by Siegmund Günther in 1877. The manuscript, a copy of Macrobius’s commentary on Cicero’s Somnium Scipionis, is located in the Bayerische Staatsbibliothek in Munich (BSB Clm 14436). It appears to date from the first quarter of the 11th century.
The graph is in the appendix, which bears the title De cursu per zodiacum (‘On the movement through the zodiac’). It was possibly added by an unknown transcriber. The graph seems to represent a plot of the inclinations of the planetary orbits as a function of the time. The zodiac is shown on a plane, with the horizontal axies showing time (divided into thirty parts), while the vertical axis shows the width of the zodiac.
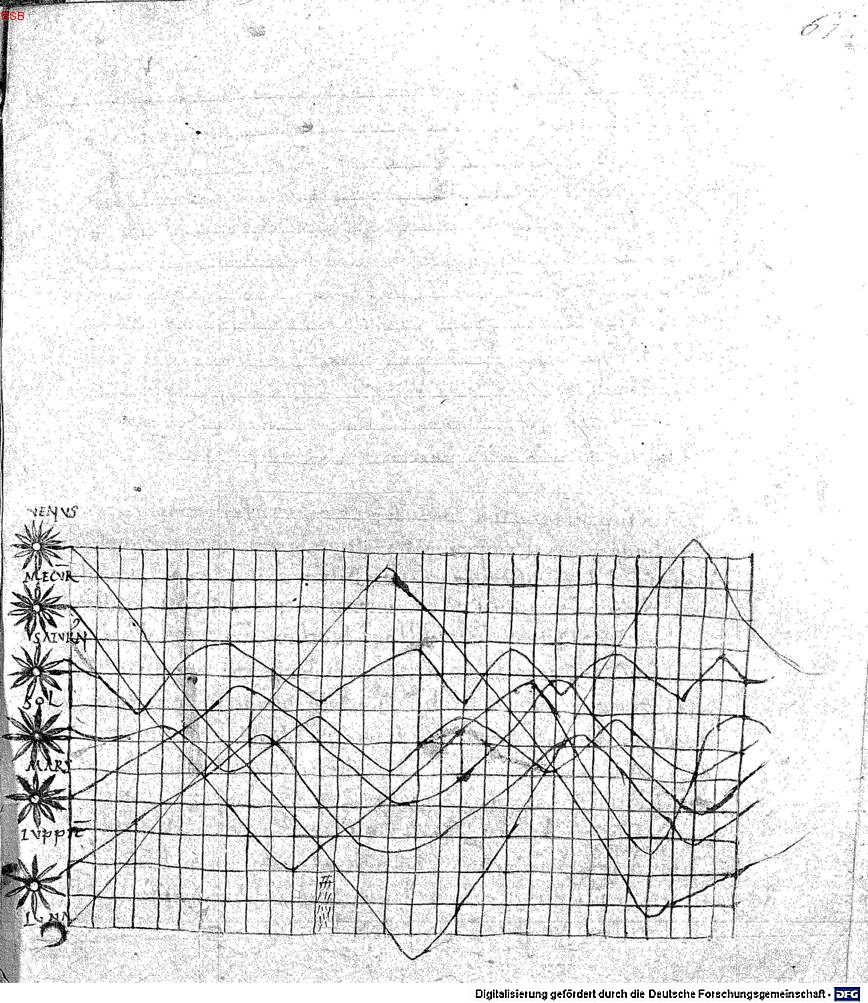
The world’s first graph?
Folio 61 recto of a copy of Macrobius’s commentary on Cicero’s ‘Somnium Scipionis’. The lines show seven heavenly bodies: Venus, Mercury, Saturn, the Sun, Mars, Jupiter, and the Moon.
Is the the world’s first graph? The use of a grid is uncannily modern. But there are some difficulties.
Each line, belonging to a different planet, is plotted on a different scale, so the periods cannot be reconciled. It would be more accurate to call it a schematic diagram of the data. In other words, the values for the amplitudes which are described in the accompanying text, cannot be read off the graph.
A final note on data visualisation: Funkhouser’s research was motivated by the explosion in the use of graphical methods in the 1930s. That’s eighty years before DJ Patil popularised the term ‘data science’.
In the run-up to the French presidential election in mid-2017, G. Elliott Morris at The Crosstab published some interesting forecasts using simulated Dirichlet draws. The post in question is no longer online. It was previously available on http://www.thecrosstab.com/2017/02/14/france-2017-methodology .
The method itself is fairly well-known (see e.g. Rigdon et al. 2009, A Bayesian Prediction Model for the U.S. Presidential Election ).
I thought it would be interesting to apply the technique when the poll samples and voter base are both tiny. So I did it for Malta, which held a snap election in June 2017. The main problem here is the inconsistency of the polls. For the last few data points, I used a series of voluntary online surveys carried out by a Facebook group calling themselves MaltaSurvey. In hindsight, the survey results appear to have been biased, but at the time there was no way of knowing how to model this bias.
So, without further ado, here is the link to the code on Github.
Airwave (2000), Innerspace
https://www.youtube.com/watch?v=FTFezae00-Q
Bibliography
Eugenio Calabi (1954), The space of Kähler metrics
Shing-Tung Yau (1978), On the Ricci curvature of a compact kähler manifold and the complex Monge-Ampère equation
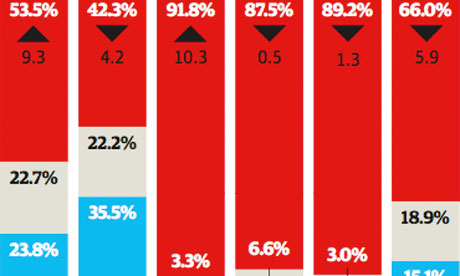
Berlin’s trendence institute surveyed over 300,000 European graduates on their perceived career prospects Illustration: Christine Oliver for the Guardian
Or what to do with millions of extra graduates.
Europe isn’t alone in facing the problem of graduate unemployment. The BRIC countries are feeling it too.
The numbers are staggering. In India one in three graduates up to the age of 29 is unemployed, according to a Labour Ministry report released last November. Total unemployment in the country is officially closer to 12%.
In China this month a record 7.26 million will graduate from the country’s universities – more than seven times the number 15 years ago.
Unemployment among new Chines graduates six months after leaving university is officially around 15%.
The real unemployment rate could be closer to 30% – some 2.3 million unemployed from this year’s graduating cohort alone, according to Joseph Cheng, professor of political science at City University of Hong Kong.
Meanwhile, back home in Europe, graduates expect to submit an average of 60 applications before landing their first job. The average wait between graduation and employment is approaching six months. That’s the average.