You may have seen the term perplexity in (countless) NLP papers and code. What is it exactly?
A bit of history
Perplexity as a metric rooted in information theory was first introduced in 1977 in the context of speech recognition by a team of IBM researchers: Frederick Jelinek, Robert L. Mercer, Lalit R. Bahl, and James K. Baker.
Perplexity — a measure of the difficulty of speech recognition tasks (JASA, 1977)
This pioneering work quantified the “difficulty” or uncertainty in probabilistic models for predicting acoustic/linguistic sequences.
The same group (Bahl, Jelinek, Mercer) continued using it, notably in their 1983 paper A maximum likelihood approach to continuous speech recognition (IEEE Trans. Pattern Anal. Mach. Intell, 1983).
It was later adapted and popularised in natural language processing through the 1990 paper
Peter F. Brown et al., “A Statistical Approach to Machine Translation” (Computational Linguistics, 1990). By this time – and these were the early days of NLP – perplexity became the standard intrinsic evaluation metric for n-gram language models. This lives on in modern LLMs, vulgarly known as PPL. Words with more than a two syllables never hurt anyone, you know.
How can we define perplexity?
Perplexity is a metric used in natural language processing (NLP) to evaluate the quality of a probabilistic language model or the fluency of generated/synthetic text. It measures how surprised or uncertain a model is when seeing a given sequence. In non-anthropomorphic language, it is a measure of the similarity of a piece of text to the text on which the model was trained.
Lower perplexity ⇒ the text is more predictable ⇒ better model / more fluent text.
Now this business of “fluent text” should be treated with caution. Just because a piece of text is different from any of the training data, it doesn’t follow that the text is not fluent. After all, we shouldn’t expect training data to contain every possible piece of text that can ever be created. (Although the massive amount of data used to train a typical LLM makes it seem like it is – and such claims are sometimes made by the so-called ‘tech industry’).
In mathematical terms: Perplexity is just exponentiated cross-entropy.
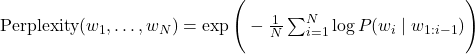
Equivalently (geometric mean form):
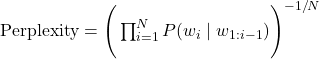
- The inner sum is the average negative log-likelihood (cross-entropy loss in nats).
- Exponentiating turns it into an intuitive “effective vocabulary size”.
The intuition behind the results is something like this:
- PPL = 10 → the model is as uncertain as if it had to choose uniformly among 10 equally likely words at every step.
- PPL = 100 → equivalent to choosing among 100 words → much more surprised.
For synthetic data: similar perplexity to real data (under the same reference model) → high statistical fidelity.
Why Use Perplexity?
- Language model evaluation on held-out text
- Synthetic data quality assessment
- Fast, automatic, and well-correlated with fluency
As always, there are limitations:
- Perplexity more or less measures fluency, not factual or semantic correctness
- It is strongly model-dependent
- Very low perplexity on synthetic data can indicate lack of diversity / copying
- Affected by context-length truncation (use sliding windows or striding)